Tag: Neural Differential Equations
-
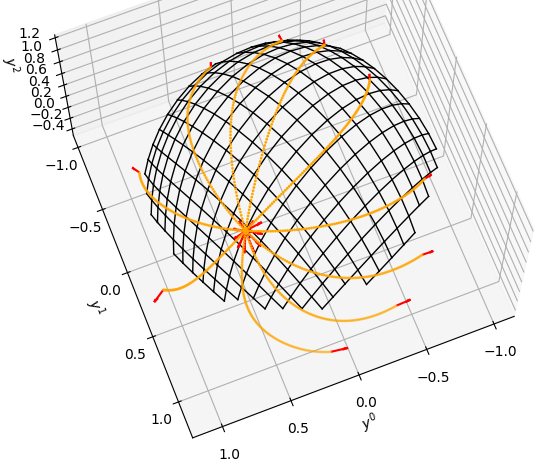
Machine learning with geodesic flows
—
by
Overview Many physical, biological and engineering systems evolve over time according to geometric laws, for example planets follow elliptical orbits shaped by gravity, and fluids swirl along streamlines governed by curvature and vorticity. A central challenge in modern machine learning is to model these dynamics faithfully and efficiently, especially in cases where the underlying structure…
-
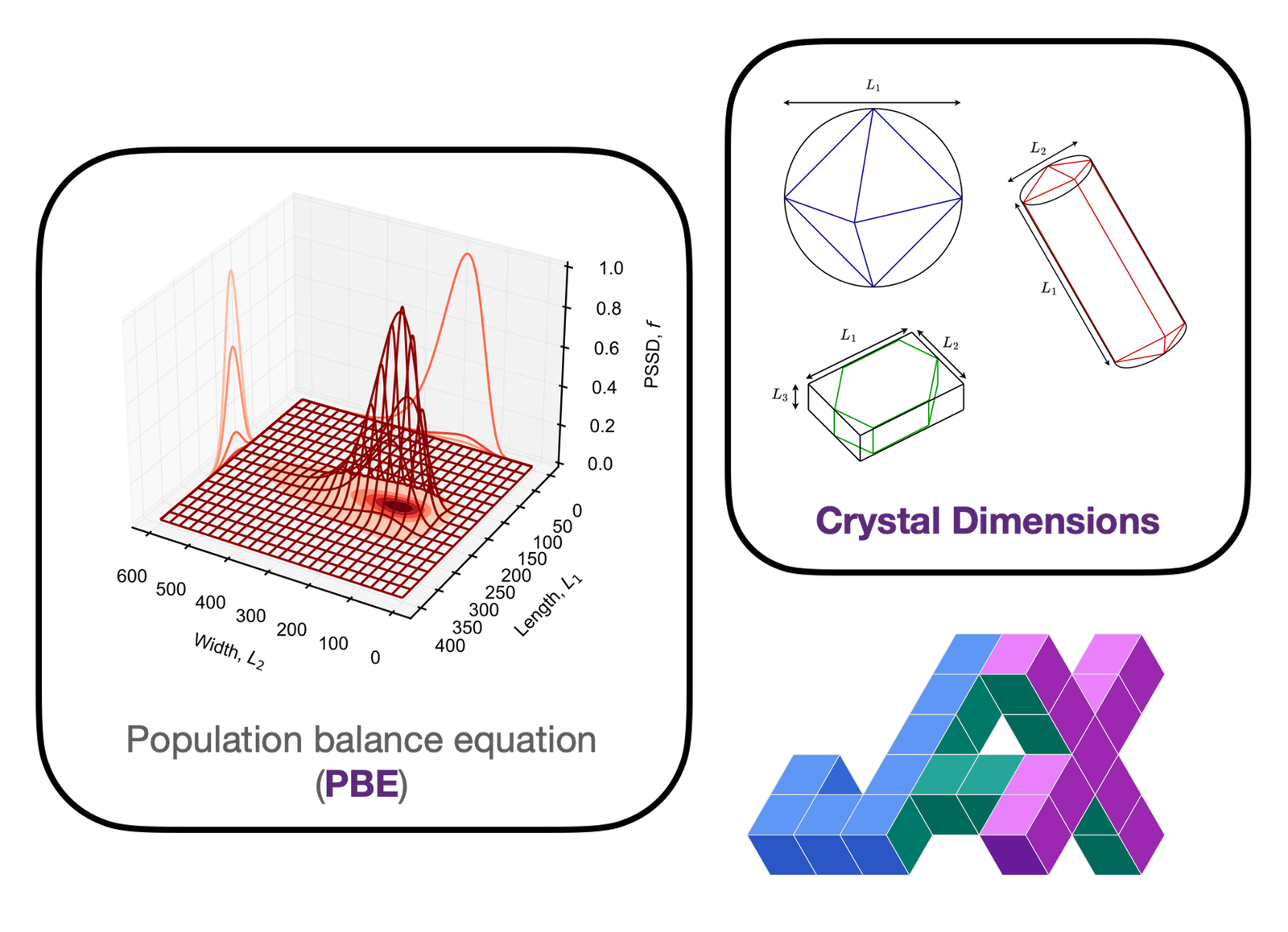
Efficient and differentiable population balance modelling with JAX
—
by
Overview Population balance equations (PBEs) are used to model the evolution of populations of particles over time, such as in crystallisation processes, chemical reactors, and biological cell growth. Solving these equations are crucial in sectors like pharmaceuticals, where they allow us to optimise manufacturing processes involving crystallisation and shorten drug development timelines. However, traditional PBE…
-
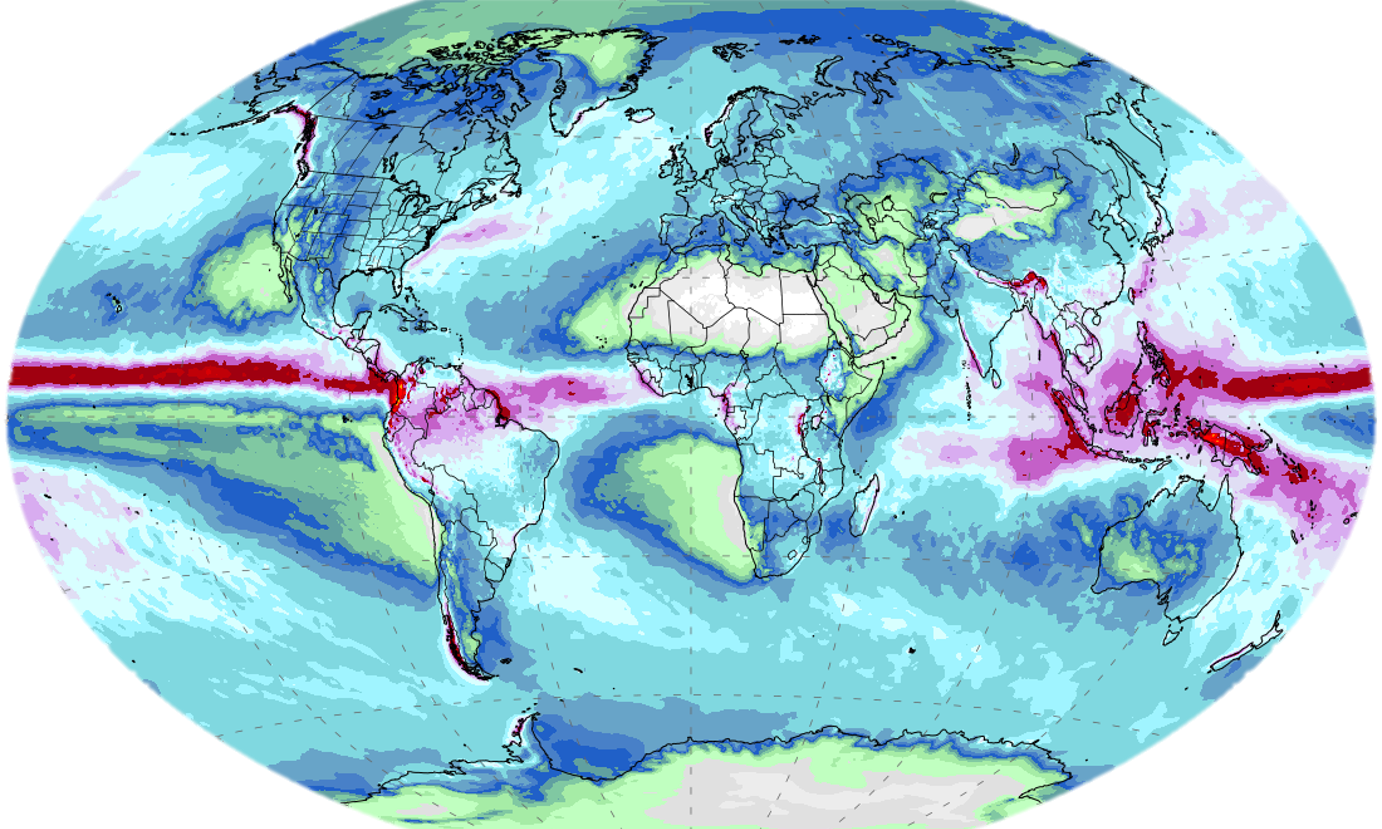
Weather and climate modelling with neural differential equations
—
by
Overview This is a new direction for the lab – more to come! Team & collaborators
