Imperial logo

Scalable SciML Lab

Machine learning with geodesic flows

—

by

Ben Moseley

Overview

Many physical, biological and engineering systems evolve over time according to geometric laws, for example planets follow elliptical orbits shaped by gravity, and fluids swirl along streamlines governed by curvature and vorticity. A central challenge in modern machine learning is to model these dynamics faithfully and efficiently, especially in cases where the underlying structure is nonlinear, high-dimensional, or only indirectly observed.

Most existing deep learning approaches to dynamics approximate trajectories in flat, Euclidean spaces and often overlook the underlying geometry of the data. This leads to models that may be expressive but lack interpretability, physical consistency, or generalisation capacity.

In this preliminary project, we introduce neural geodesic flows – a new class of machine learning models that learn to predict dynamical systems by assuming the system evolves along the geodesics of a learned latent Riemannian manifold. This approach constrains the model with structure-preserving geometric properties that adapt naturally to complex dynamics.

Research highlights

Neural geodesic flows

To predict the dynamics of a system, we first map observations (such as the positions of two planets, or the velocity of a fluid) to coordinates on a latent manifold. Next, we evolve the coordinates over time by moving the system along geodesics (locally length-minimising curves) on the manifold. This is done by solving the geodesic flow equations on the manifold. Finally, we map the manifold coordinates back to the observation (data) space to predict the dynamics.

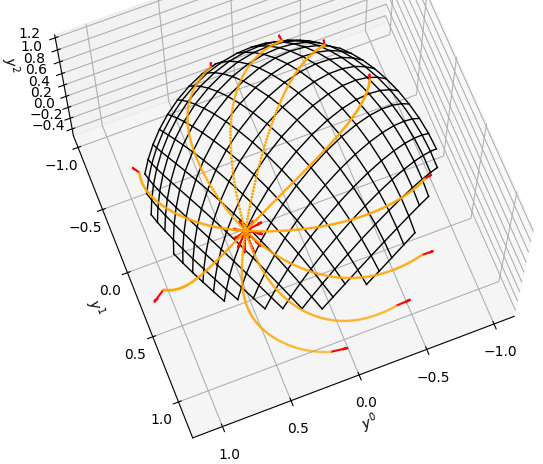
Importantly, we jointly learn the mapping back and forth between observations and coordinates on the latent manifold, as well as the metric of the manifold, by representing them with deep neural networks and training the model to match example trajectories of the system in the data space. An example of our model learning the toy dynamics of particles flowing over the surface of a sphere is shown in Fig. 1.

Fig. 1: A toy example learning the dynamics of particles flowing over the surface of a sphere. Our model maps observations of the particles in x,y,z (left) to coordinates on a latent manifold (in this case, a sphere) (right). It then evolves the coordinates along geodesics of the latent manifold, before mapping them back to the original data space.

We call this model a neural geodesic flow and its schematic is shown in Fig. 2.

Fig. 2: A schematic of a neural geodesic flow. Here, y represents observations in the data space, z represents coordinates on the latent manifold, and F represents the mapping between them.

Our core assumption is that the observed data evolves along geodesics of a latent manifold. This may seem strong, but multiple physical systems can be interpreted in this way, including classical mechanics and spacetime evolution in general relativity, with deep links to the principle of least action. By construction our model naturally conserves geodesic energy, which, when trained, can lead to good total energy conservation. An example of our model learning to model the motion of two bodies orbiting each other is shown in Fig. 3.

Fig. 3: A neural geodesic flow modelling the two-body problem.

Applications and impact

Neural geodesic flows are designed to model the intrinsic geometrical structure of complex dynamical data. Future applications could include learning latent physics models, compressing simulations to low-dimensional embeddings, and more generally advancing manifold learning models.

Future directions

This is a preliminary project and we actively working on improving this model. Please contact us if you are interested in contributing / learning more about this project.

Publications

Julian Bürge. Neural Geodesic Flows. Master’s Thesis, ETH Zurich (2025).

Resources

Neural Geodesic Flows GitHub repo

Team & collaborators

  • Julian Bürge: ETH Zurich.
  • Siddhartha Mishra: ETH Zurich.
  • Ben Moseley: Imperial College London.
  • Lewis O’Donnell: Imperial College London.

More projects