Overview

Quantum theory is incredibly powerful for predicting the probabilities of what we’ll see in experiments, but it cannot tell us the certain outcome of a single experiment. That is to say, current quantum theory states that the universe is inherently random. Whether or not this is the case, and whether it is possible for quantum theory to predict certain outcomes, has been a topic of intense debate, with figures such as Einstein suggesting the theory might be incomplete.

Extensions of quantum theory have been proposed which try to predict the outcomes of experiments deterministically. Such proposals often involve introducing local hidden variables (LHVs) – underlying properties of a quantum system we don’t currently see that could explain outcomes deterministically. LHV models often rely on two other assumptions: locality (no faster-than-light influences) and free choice of experimenters to set their measurement devices.

Bell proved that such theories, if they exist, would mean quantum systems obey a certain inequality – but two decades later Bell’s inequality was successfully broken by experiment, suggesting to many that LHV theories were impossible.

In this project, we are taking a fresh look at an alternative deterministic quantum theory and using AI and scientific machine learning to provide key insights into this theory.

Research highlights

Quantum experiments as games

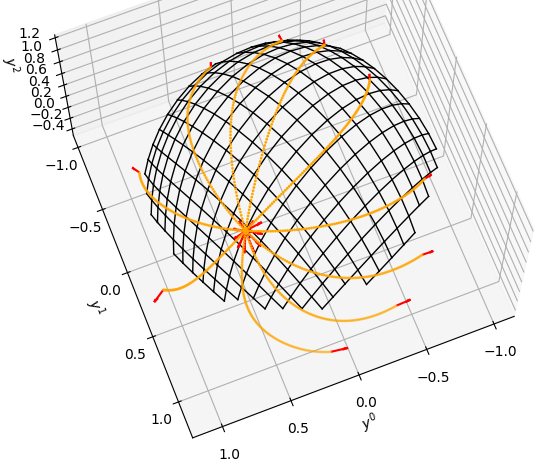
In light of the limitations of LHV theories, recent work by Fourny and Baczyk and Fourny proposed an alternative deterministic extension to quantum theory, by framing the measurement of quantum experiments as a game between observers and the universe (Fig. 1).

In their proposed game, the players take turns – first, an observer (or multiple observers) decides what aspect of a quantum system they want to measure (for example, the spin of a particle). Then, Nature choses an outcome from a possible set of measurement outcomes. At the end of the game, all players receive a reward, and the players decide upon their previous actions to maximise this reward. Crucially, given the fixed game and rewards, the optimal game strategies (and therefore resulting measurement outcomes) can be deterministically predicted.

Such a theory can be thought of as a LHV theory where the rewards are the “unseen” variables of the quantum system. Thus, Bell’s inequality could still rule out this theory. However, to ensure Bell’s inequality remains broken, the researchers relax the free choice assumption made by previous LHV theories. In particular, they assert that players operate under contingent free choice, where players can perfectly anticipate each other’s reasoning. The researchers show that this game mandate enables the game’s outcomes to match standard quantum theory and experimental predictions.

Learning rewards with AI

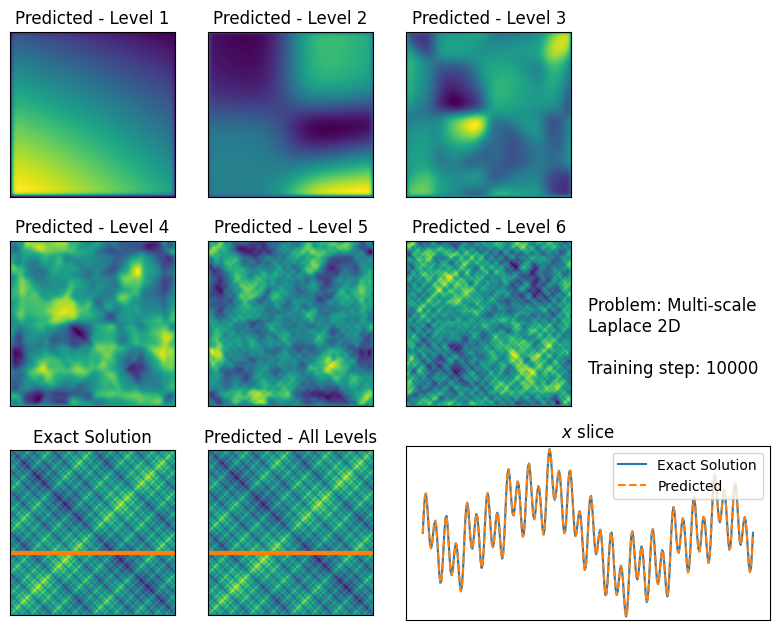
Whilst promising, the theory is currently missing a critical insight; it is not known how to derive or write down the rewards each player receives for a specific quantum experiment. In this project, instead of trying to mathematically derive reward-generating equations from a hidden variable theory – which seems challenging right now, we are training AI to predict these rewards (Fig. 2).

To train the AI model to predict rewards, we wrote a differentiable game solver which, given a quantum experiment and predicted rewards from the AI model, provided a set of predicted measurement outcomes. We then updated the AI model so that the predictions matched the probability of measurement outcomes predicted by standard quantum theory.

Applications and impact

Our AI model was able to learn rewards for several simple experiments (including the famous EPR experiment) which resulted in measurement outcomes that closely matched predictions from standard quantum theory. Notably, the method was able to learn rewards for the EPR experiment such that the measurement outcomes successfully violated the Bell inequality. These results show that this extension theory can exceed classical physics and successfully reproduce quantum phenomena, and could eventually enable us to make verifiable predictions with real-world experiments.

Future directions

In our future work, we aim to learn rewards for more complex quantum experiments and gain theoretical insight into the game rewards. This is a preliminary project we are actively working on.

Contact / get involved

Please contact us if you are interested in contributing / learning more about this project.

Publications

Florian Pauschitz. Extending quantum theory with an AI-supported approach. Master’s Thesis, ETH Zurich (2025).

Resources

Team & collaborators

• Florian Pauschitz: ETH Zurich.
• Ghislain Fourny: ETH Zurich.
• Ben Moseley: Imperial College London.