Overview
Physics-informed neural networks (PINNs) have emerged as a promising tool for solving differential equations. They have been applied to many scientific problems and a large number of approaches extending their capabilities have been proposed. PINNs work by using a neural network to directly approximate the solution and training it to satisfy the differential equation.
However, a well-known limitation of PINNs is that they often struggle when solving equations with highly multi-scale solutions. This is primarily due to the spectral bias inherent in neural networks (their tendency to learn high frequencies much slower than low frequencies) and the complexity of optimising them over large, complex domains.
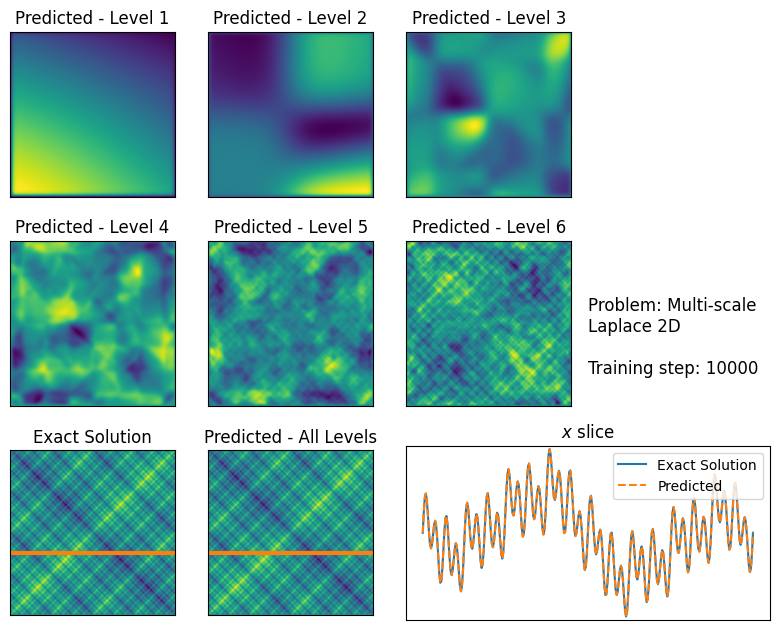
Our lab is extending PINNs by combining them with domain decomposition, drawing inspiration from classical finite element and Schwarz domain decomposition methods. We find that this “divide and conquer” strategy significantly improves their computational efficiency and accuracy when solving multi-scale problems (Fig. 1). Our long-term goal is to design scalable PINNs which can solve arbitrarily complex multi-scale problems.

Research highlights
Finite basis physics-informed neural networks
Our first step was to introduce finite basis PINNs (FBPINNs), which decompose the modelling domain into overlapping subdomains. We place a separate PINN in each subdomain, and collectively train them to solve the larger equation (Fig. 2). We found that this “divide and conquer” strategy improves computational efficiency and accuracy when solving multi-scale wave and Laplace’s equation problems (Fig. 1).

Multilevel domain decomposition architectures
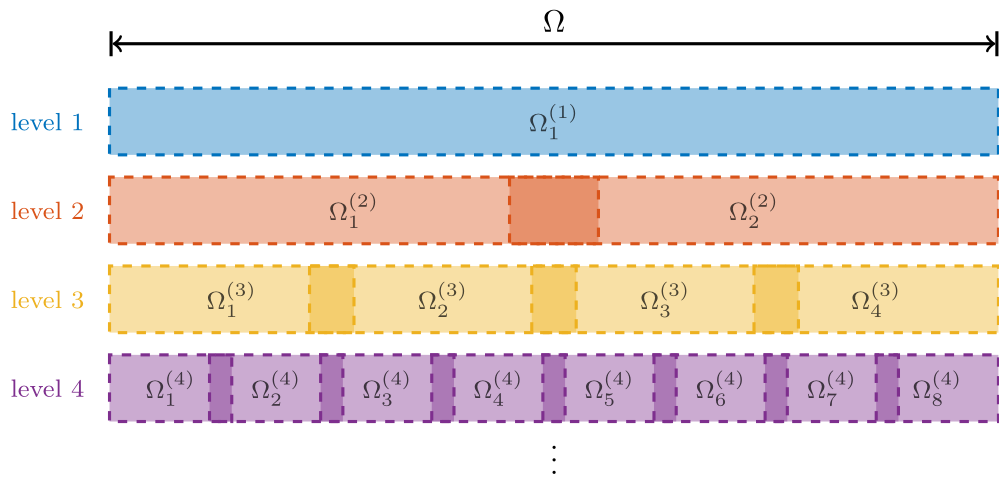
For large problems, we found that FBPINNs can still struggle to train, likely because it becomes challenging to communicate effectively between subdomains. To overcome this, we developed multilevel FBPINNs, inspired by classical multilevel Schwarz domain decomposition methods. This approach introduces a hierarchy of domain decompositions (Fig. 3), where coarser levels facilitate global communication between subdomains. We found that multilevel FBPINNs further improve performance when solving highly multi-scale problems (Fig. 4).
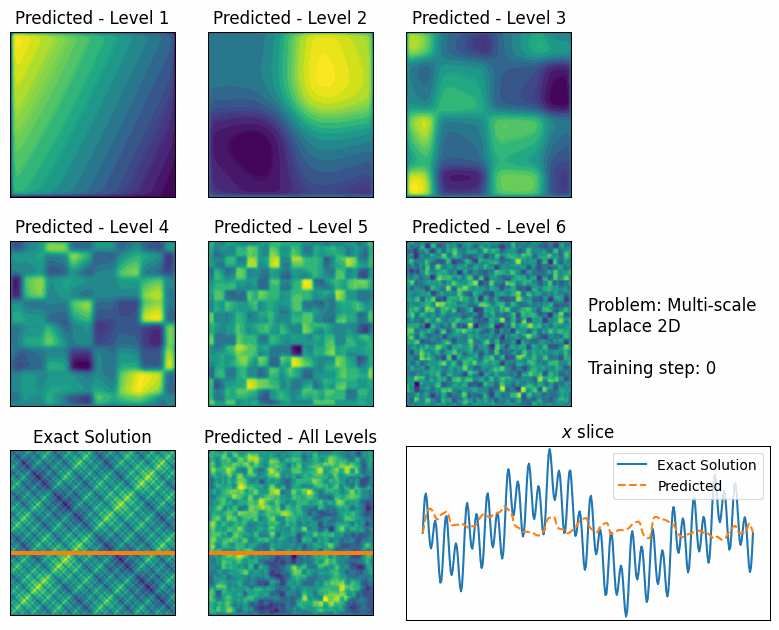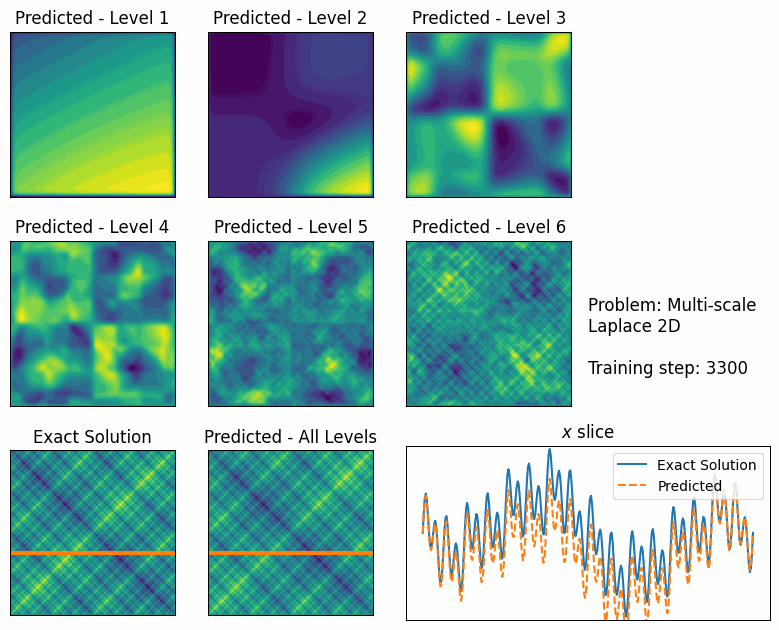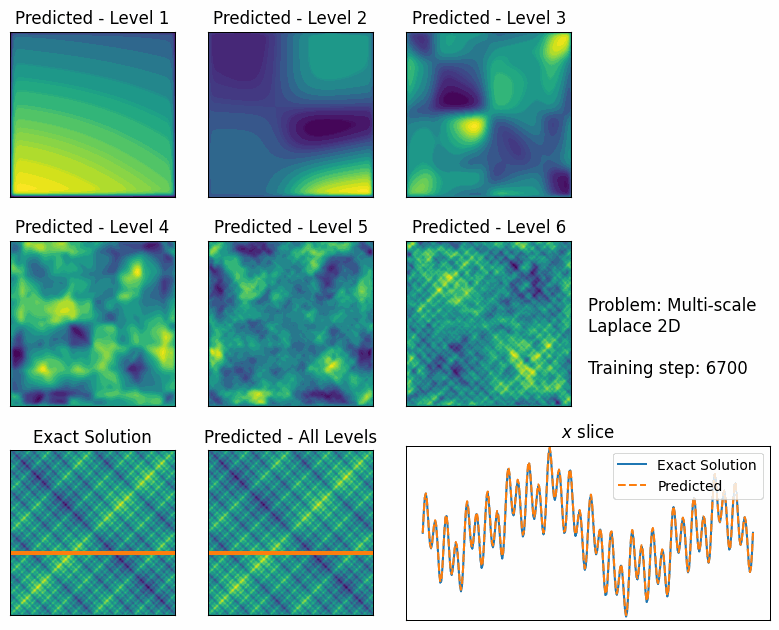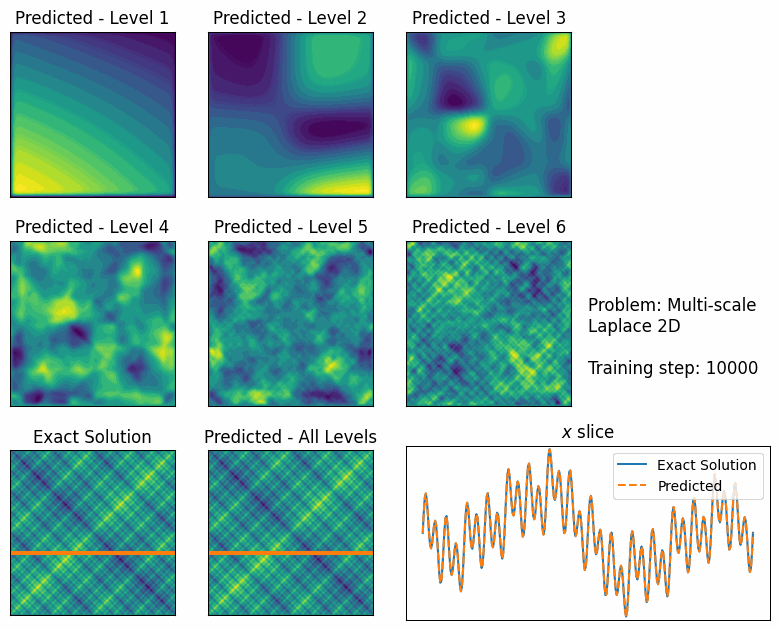
Applications and impact
Overall, FBPINNs and their multilevel variants significantly improve the performance of PINNs on multi-scale problems. We have released an open-source FBPINN library which has been used by 100s of researchers to solve various differential equations across science.
Yet, even with our methods, in many cases (FB)PINNs remain computationally expensive to train compared to traditional numerical methods. Our long-term goal is to make PINNs competitive with traditional numerical methods by enabling them to scale to arbitrarily complex problems.
Future directions
Our future work includes:
- Accelerating FBPINNs using a multi-GPU implementation.
- Improving convergence by investigating novel optimisation methods.
- Using adaptive domain decomposition to improve accuracy and efficiency, inspired by traditional mesh-refinement.
- Applying FBPINNs to practical problems in physics and engineering by collaborating with domain experts.
Contact / get involved
Please contact us if you are interested in contributing / learning more about this project.
Publications
Ben Moseley, Andrew Markham, Tarje Nissen-Meyer. “Finite Basis Physics-Informed Neural Networks (FBPINNs): A Scalable Domain Decomposition Approach for Solving Differential Equations.” Advances in Computational Mathematics (2023).
Victorita Dolean, Alexander Heinlein, Siddhartha Mishra, Ben Moseley. “Multilevel Domain Decomposition-Based Architectures for Physics-Informed Neural Networks.” Computer Methods in Applied Mechanics and Engineering (2024).
Resources
Team & collaborators
- Ben Moseley: Imperial College London.
- Andrew Markham: University of Oxford.
- Tarje Nissen-Meyer: University of Oxford.
- Siddhartha Mishra: ETH Zurich.
- Victorita Dolean: Eindhoven University of Technology.
- Alexander Heinlein: Delft University of Technology.
- Samuel Anderson: University of Strathclyde.
- Jennifer Pestana: University of Strathclyde.
- Jan Willem van Beek: Eindhoven University of Technology.
- Philéas Grenade: Imperial College London.